15  SHAP with XGBoost (Titanic Dataset)

import xgboost
import shap
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

# Import machine learning methods
from sklearn.model_selection import train_test_split
from xgboost import XGBClassifier
from lightgbm import LGBMClassifier
from sklearn.ensemble import RandomForestClassifier

# Import shap for shapley values
import shap

# JavaScript Important for the interactive charts later on
shap.initjs()
download_required = True

if download_required:

    # Download processed data:
    address = 'https://raw.githubusercontent.com/MichaelAllen1966/' + \
                '1804_python_healthcare/master/titanic/data/processed_data.csv'

    data = pd.read_csv(address)

    # Create a data subfolder if one does not already exist
    import os
    data_directory ='./datasets/'
    if not os.path.exists(data_directory):
        os.makedirs(data_directory)

    # Save data
    data.to_csv(data_directory + 'processed_data.csv', index=False)

data = pd.read_csv('datasets/processed_data.csv')
# Make all data 'float' type
data = data.astype(float)

# Use `survived` field as y, and drop for X
y = data['Survived'] # y = 'survived' column from 'data'
X = data.drop('Survived', axis=1) # X = all 'data' except the 'survived' column

# Drop PassengerId
X.drop('PassengerId',axis=1, inplace=True)

X_train, X_test, y_train, y_test = train_test_split(X,
                                                    y,
                                                    random_state=42,
                                                    test_size=0.25)

model = XGBClassifier(random_state=42)
model.fit(X_train, y_train)

# Predict training and test set labels
y_pred_train = model.predict(X_train)
y_pred_test = model.predict(X_test)

# Predict probabilities of survival
y_prob_train = model.predict_proba(X_train)
y_prob_test = model.predict_proba(X_test)

accuracy_train = np.mean(y_pred_train == y_train)
accuracy_test = np.mean(y_pred_test == y_test)

print (f'Accuracy of predicting training data = {accuracy_train:.2%}')
print (f'Accuracy of predicting test data = {accuracy_test:.2%}')
Accuracy of predicting training data = 97.31%
Accuracy of predicting test data = 80.72%
# explain the model's predictions using SHAP
explainer = shap.Explainer(model, X_train)
shap_values = explainer(X_test)

shap_values
.values =
array([[-0.41472028, -0.82758431,  0.08631781, ...,  0.        ,
         0.        ,  0.        ],
       [ 0.34368675,  0.01027041,  0.20749824, ...,  0.        ,
         0.        ,  0.        ],
       [-0.49629094, -0.24858944, -0.07239207, ...,  0.        ,
         0.        ,  0.        ],
       ...,
       [-0.45505765, -0.95988004,  0.14636154, ...,  0.        ,
         0.        ,  0.        ],
       [ 1.38846514, -0.87314281,  0.06420199, ...,  0.        ,
         0.        ,  0.        ],
       [-0.51810456, -1.0059387 ,  0.18350499, ...,  0.        ,
         0.        ,  0.        ]])

.base_values =
array([-0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838, -0.81725838, -0.81725838,
       -0.81725838, -0.81725838, -0.81725838])

.data =
array([[ 3., 28.,  1., ...,  0.,  0.,  1.],
       [ 2., 31.,  0., ...,  0.,  0.,  1.],
       [ 3., 20.,  0., ...,  0.,  0.,  1.],
       ...,
       [ 3., 28.,  0., ...,  0.,  0.,  1.],
       [ 2., 24.,  0., ...,  0.,  0.,  1.],
       [ 3., 18.,  1., ...,  0.,  0.,  1.]])
shap_values_numeric = shap_values.values
shap_values_numeric
array([[-0.41472028, -0.82758431,  0.08631781, ...,  0.        ,
         0.        ,  0.        ],
       [ 0.34368675,  0.01027041,  0.20749824, ...,  0.        ,
         0.        ,  0.        ],
       [-0.49629094, -0.24858944, -0.07239207, ...,  0.        ,
         0.        ,  0.        ],
       ...,
       [-0.45505765, -0.95988004,  0.14636154, ...,  0.        ,
         0.        ,  0.        ],
       [ 1.38846514, -0.87314281,  0.06420199, ...,  0.        ,
         0.        ,  0.        ],
       [-0.51810456, -1.0059387 ,  0.18350499, ...,  0.        ,
         0.        ,  0.        ]])

16 SHAP - importance table

# Calculate mean Shap value for each feature in training set
importances = pd.DataFrame()
importances['features'] = X.columns.tolist()
importances['mean_shap_values'] = np.mean(shap_values_numeric, axis=0)

# Calculate mean absolute Shap value for each feature in training set
# This will give us the average importance of each feature
importances['mean_abs_shap_values'] = np.mean(
    np.abs(shap_values_numeric),axis=0)

importances['rank_shap'] = importances['mean_abs_shap_values'].rank(ascending=False).values
importances.sort_values('rank_shap').head()
features mean_shap_values mean_abs_shap_values rank_shap
10 male 0.047098 1.872651 1.0
0 Pclass 0.268006 1.072309 2.0
4 Fare 0.084978 0.914949 3.0
1 Age -0.325160 0.846433 4.0
8 CabinNumber 0.126974 0.344576 5.0

17 SHAP Plots

shap.plots.bar(shap_values)

# visualize the first prediction's explanation
shap.plots.waterfall(shap_values[0])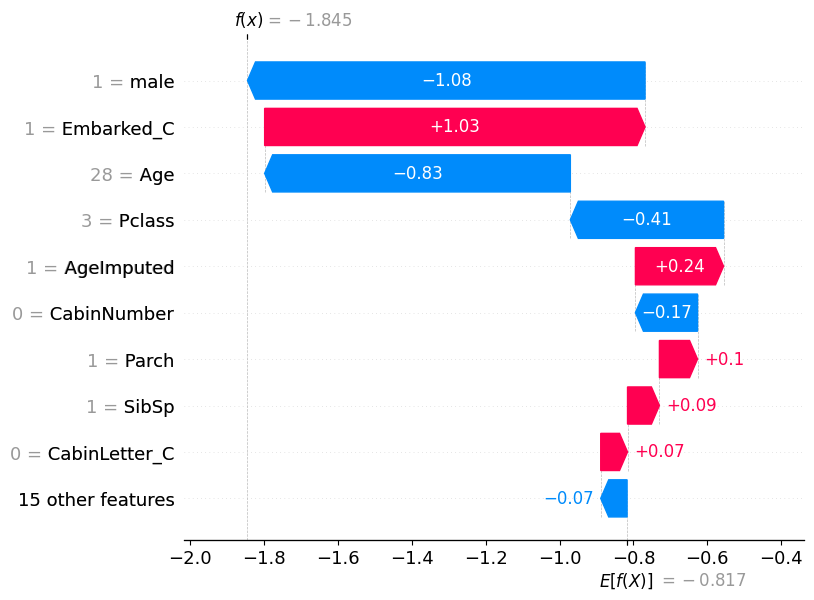

X_test[['male', 'Embarked_C', 'Age', 'Pclass']]
male Embarked_C Age Pclass
709 1.0 1.0 28.0 3.0
439 1.0 0.0 31.0 2.0
840 1.0 0.0 20.0 3.0
720 0.0 0.0 6.0 2.0
39 0.0 1.0 14.0 3.0
... ... ... ... ...
880 0.0 0.0 25.0 2.0
425 1.0 0.0 28.0 3.0
101 1.0 0.0 28.0 3.0
199 0.0 0.0 24.0 2.0
424 1.0 0.0 18.0 3.0

223 rows × 4 columns

# visualize another prediction's explanation
shap.plots.waterfall(shap_values[7])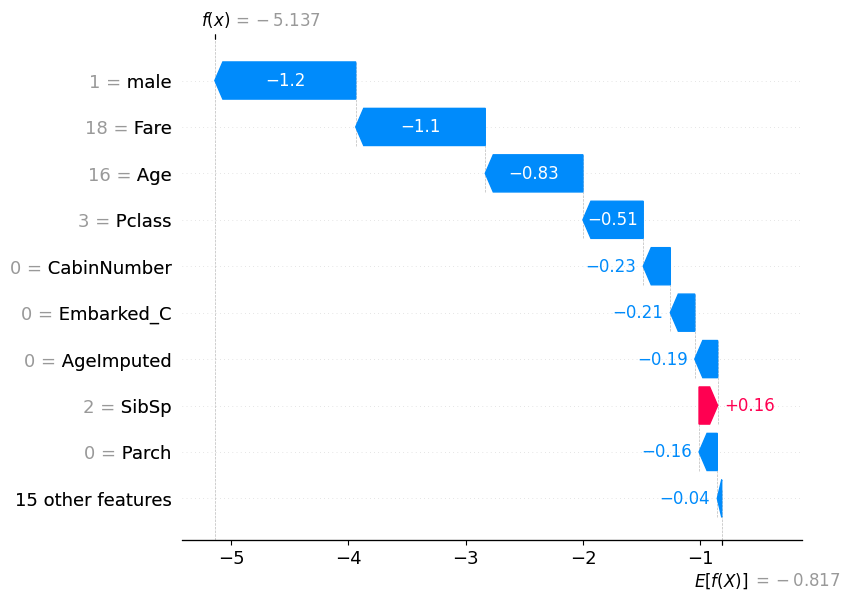

17.0.0.1 Find examples with high or low probabilities

highest_prob = pd.Series(y_pred_test).sort_values(ascending=False).head(1)
highest_prob
69    1
dtype: int32
high_prob_index = highest_prob.index[0]
shap.plots.waterfall(shap_values[high_prob_index])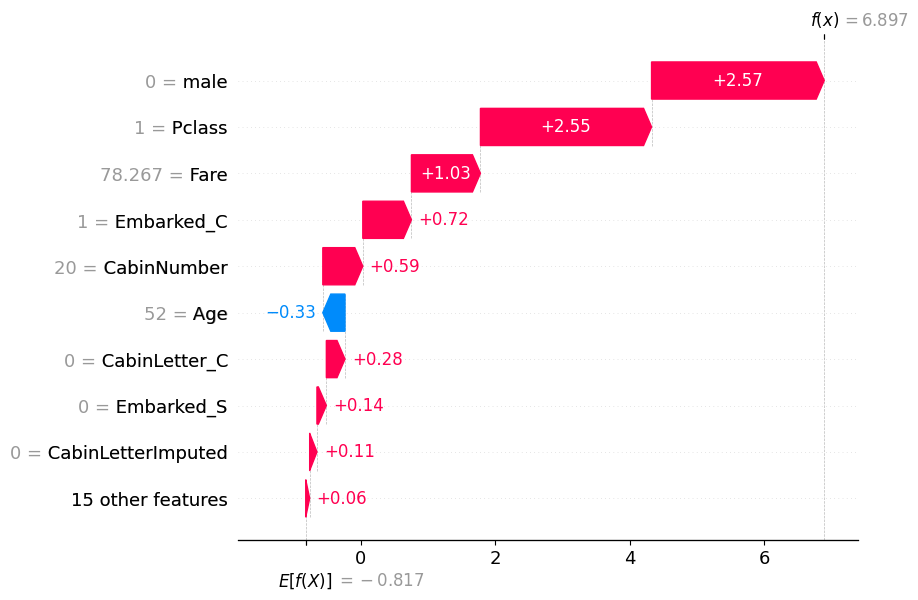

low_prob = pd.Series(y_pred_test).sort_values(ascending=False).tail(1)
low_prob
222    0
dtype: int32
low_prob_index = low_prob.index[0]
shap.plots.waterfall(shap_values[low_prob_index])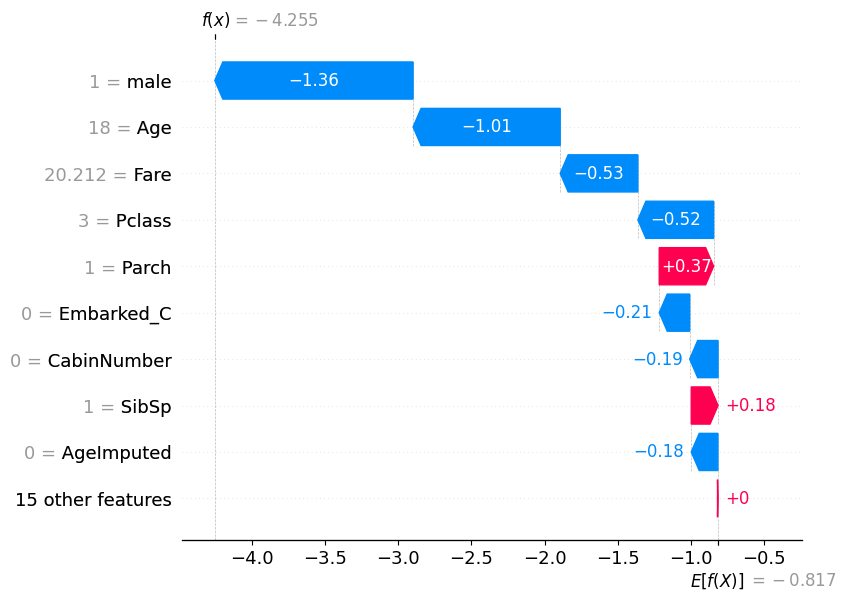

17.1 Force plots

# visualize the first prediction's explanation with a force plot
shap.plots.force(shap_values[0])
Visualization omitted, Javascript library not loaded!
Have you run `initjs()` in this notebook? If this notebook was from another user you must also trust this notebook (File -> Trust notebook). If you are viewing this notebook on github the Javascript has been stripped for security. If you are using JupyterLab this error is because a JupyterLab extension has not yet been written. 
# visualize all the predictions
shap.plots.force(shap_values)
Visualization omitted, Javascript library not loaded!
Have you run `initjs()` in this notebook? If this notebook was from another user you must also trust this notebook (File -> Trust notebook). If you are viewing this notebook on github the Javascript has been stripped for security. If you are using JupyterLab this error is because a JupyterLab extension has not yet been written.

17.2 Dependence Plots

# create a dependence scatter plot to show the effect of a single feature across the whole dataset
shap.plots.scatter(shap_values[:, "Age"])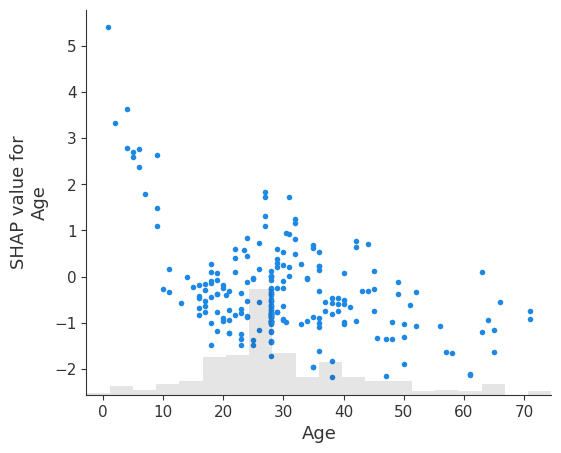

shap.plots.scatter(shap_values[:, "Age"], color=shap_values[:, "male"])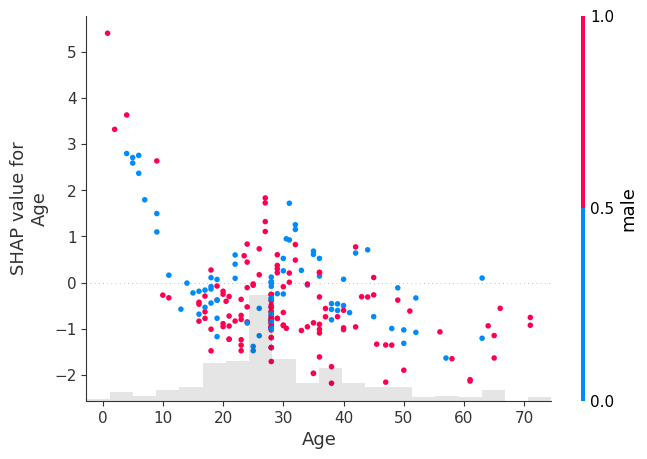

shap.plots.scatter(shap_values[:, "Age"], color=shap_values[:, "Pclass"])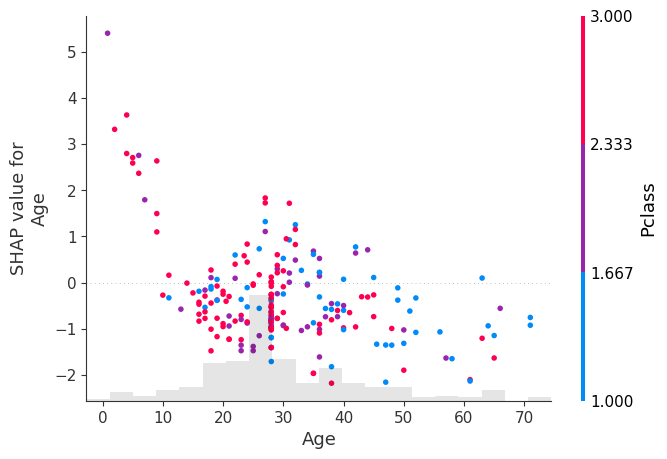

shap.plots.scatter(shap_values[:, "Age"], color=shap_values[:, "Fare"])

shap.plots.scatter(shap_values[:, "Age"], color=shap_values)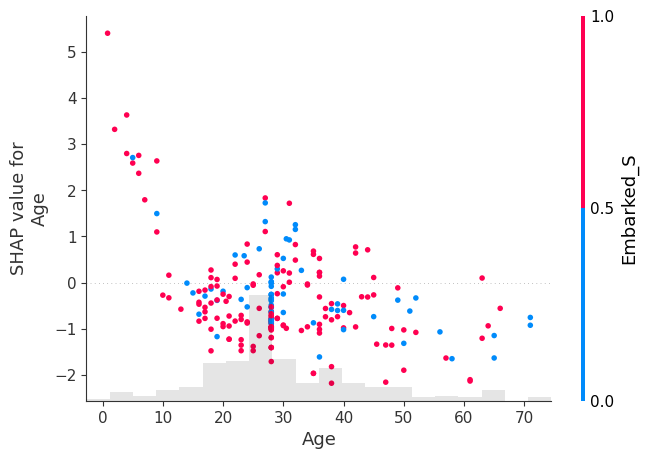

shap.plots.scatter(shap_values[:, "Fare"], color=shap_values)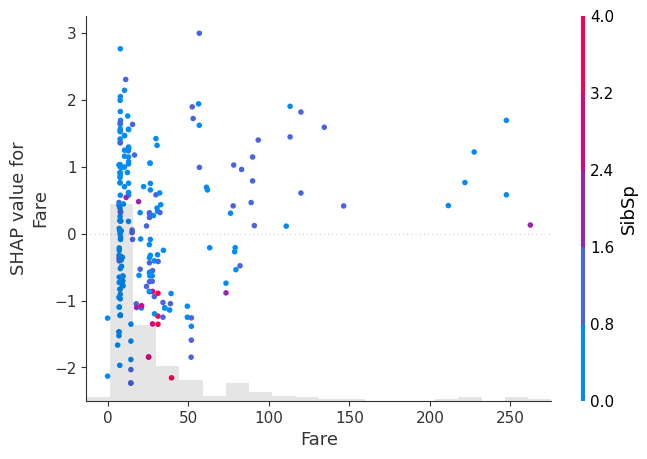

shap.plots.scatter(shap_values[:, "male"], color=shap_values)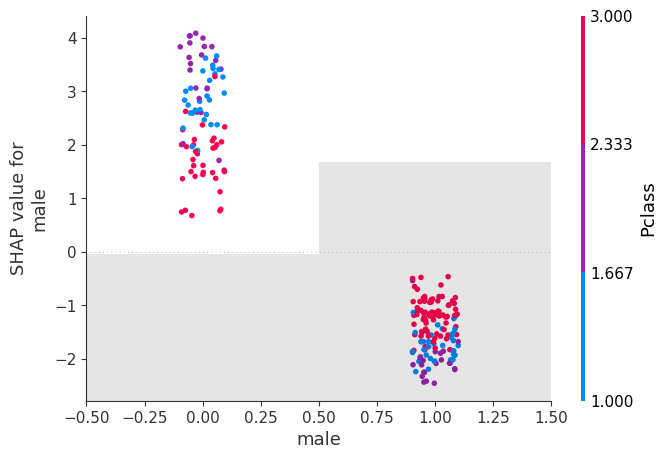

shap.plots.scatter(shap_values[:, "male"], color=shap_values)

17.3 Beeswarm

# summarize the effects of all the features
shap.plots.beeswarm(shap_values)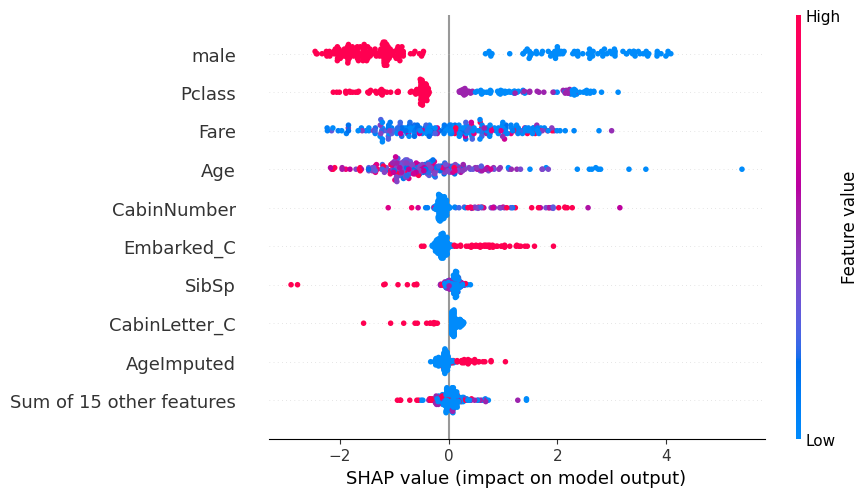

17.4 Violin

# summarize the effects of all the features
shap.plots.violin(shap_values)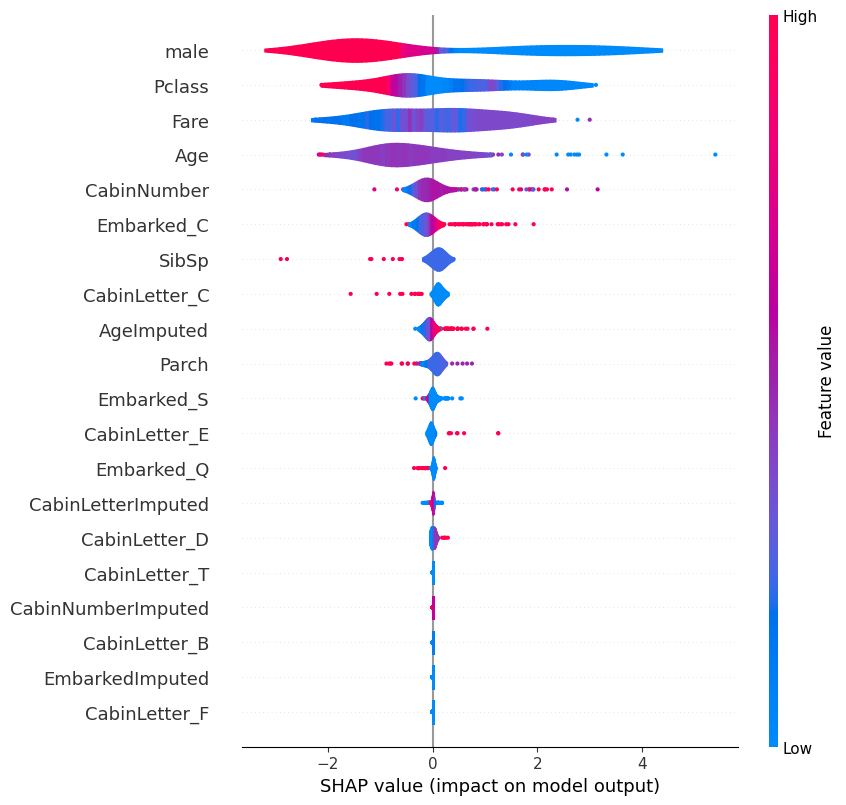

17.4.1 Bar: Cohorts

sex = ["Women" if shap_values[i, "male"].data == 0 else "Men" for i in range(shap_values.shape[0])]
shap.plots.bar(shap_values.cohorts(sex).abs.mean(0))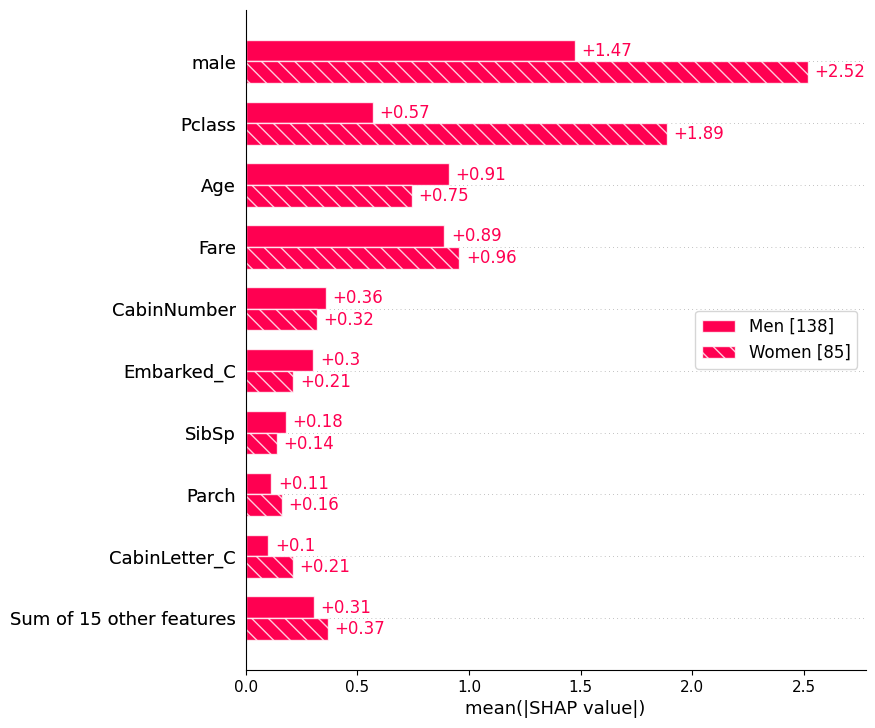

Plot the bars for an individual.

shap.plots.bar(shap_values[1])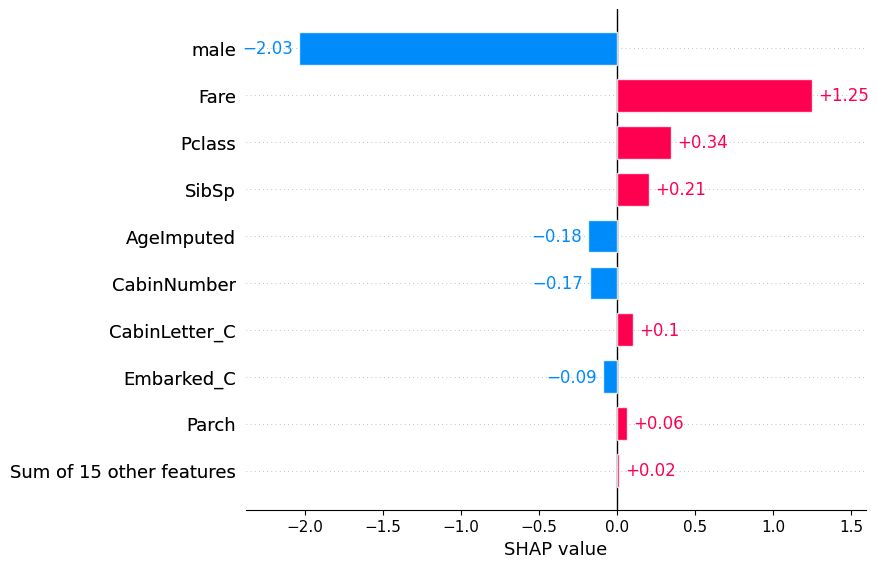

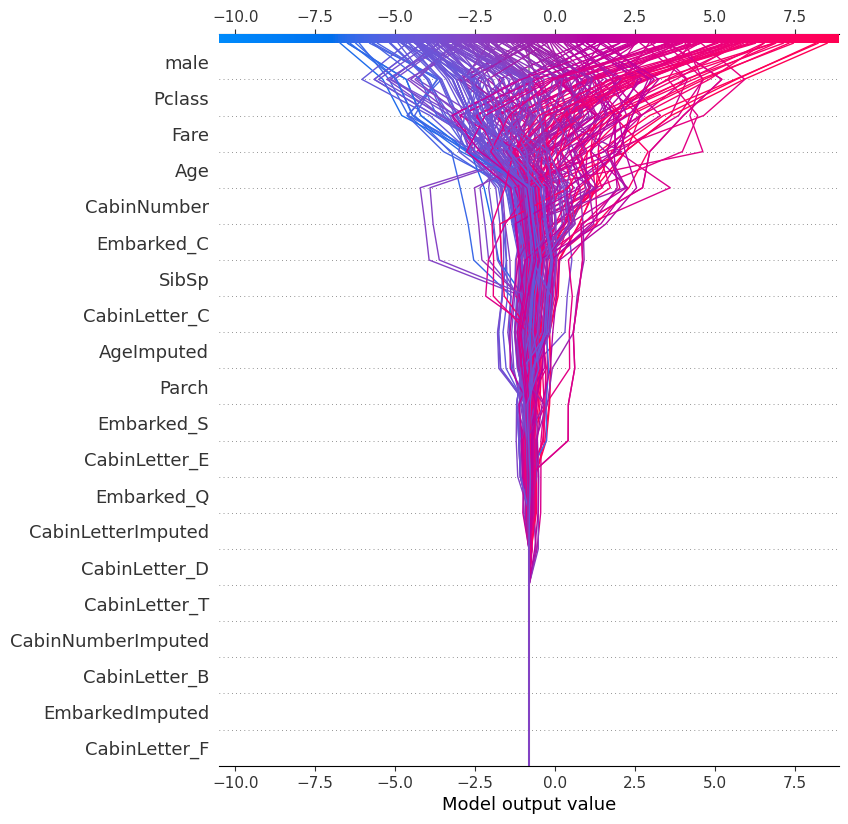
18 Decision

shap.plots.decision(
    explainer.expected_value,
    shap_values.values,
    feature_names=X.columns.tolist()
    )

18.0.1 Decision plot for individual

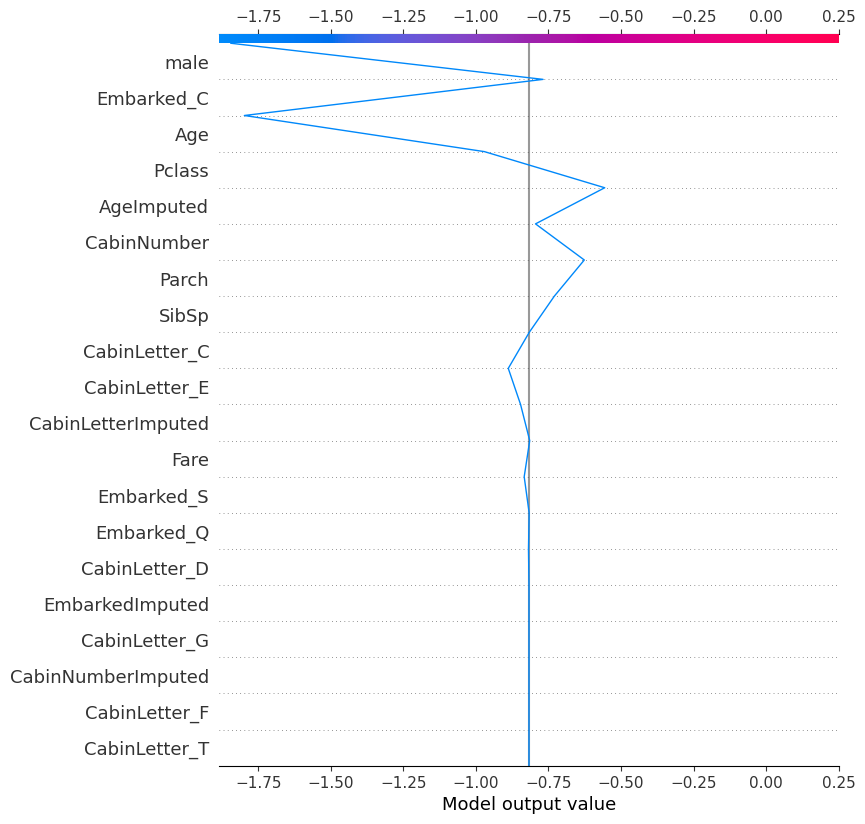
shap.plots.decision(
    explainer.expected_value,
    explainer.shap_values(X_test)[0], # one way of specifying the record to look at
    feature_names=X.columns.tolist()
    )

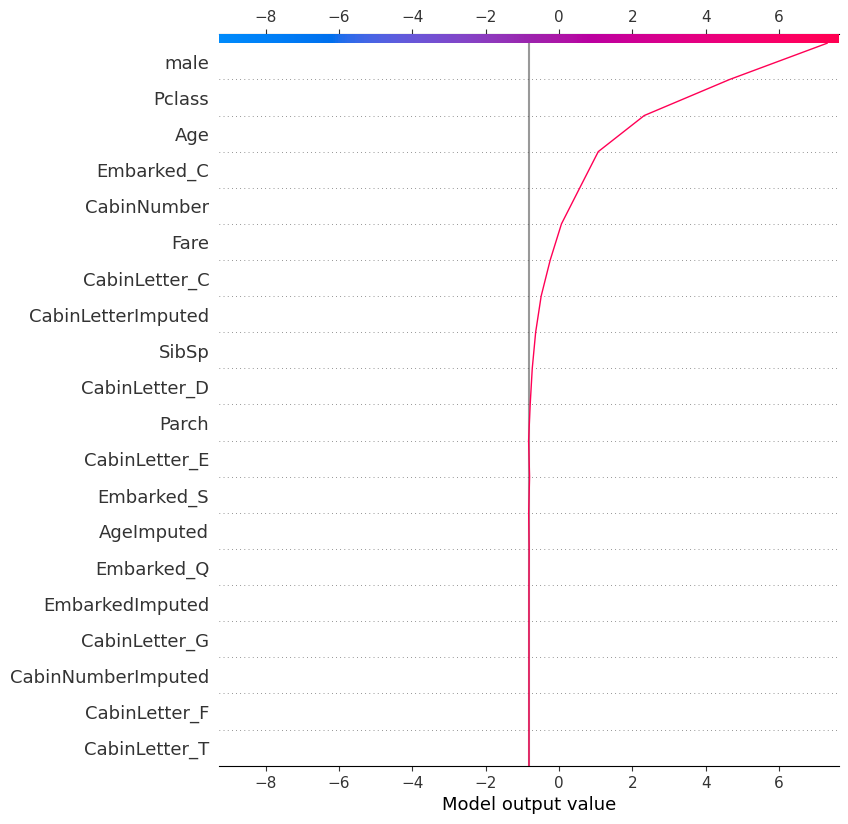
shap.plots.decision(
    explainer.expected_value,
    shap_values.values[121], # another way of specifying the record to look at
    feature_names=X.columns.tolist()
    )

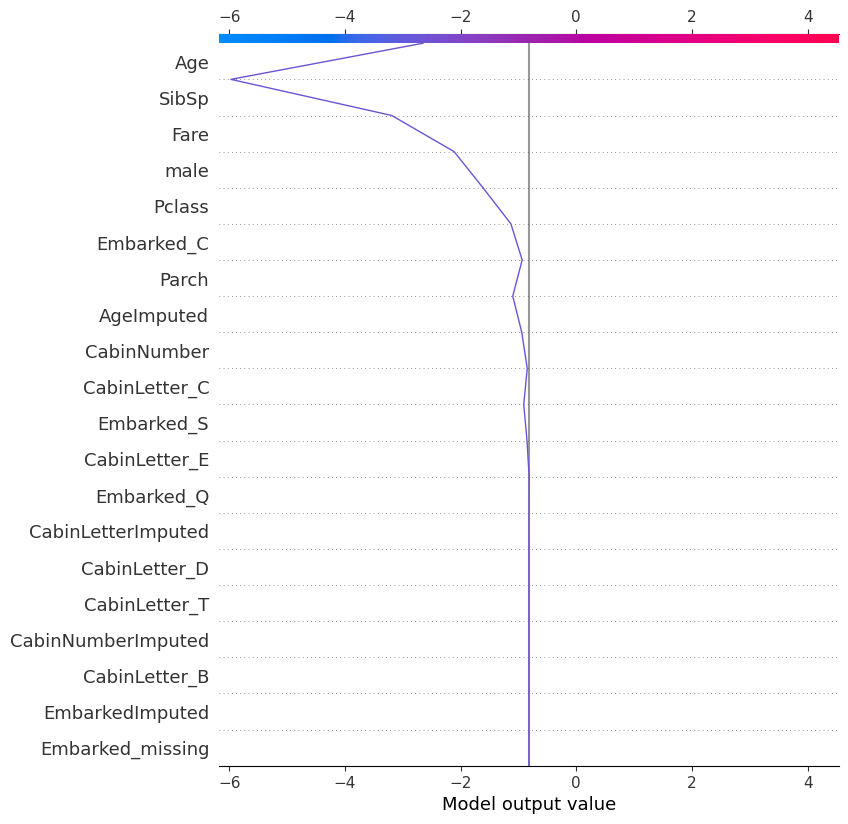
shap.plots.decision(
    explainer.expected_value,
    explainer.shap_values(X_test)[215],
    feature_names=X.columns.tolist()
    )

18.1 SHAP: Probability Alternative

Recalculate the SHAP values as changes in probability instead of log odds.

# explain the model's predictions using SHAP
explainer_probability = shap.Explainer(model, X_train, model_output="probability")
shap_values_probability = explainer_probability(X_test)

shap_values_probability
.values =
array([[-0.05238777, -0.13358663,  0.01009056, ...,  0.        ,
         0.        ,  0.        ],
       [ 0.0511844 , -0.03143588,  0.0286387 , ...,  0.        ,
         0.        ,  0.        ],
       [-0.05579166, -0.05355721, -0.00460973, ...,  0.        ,
         0.        ,  0.        ],
       ...,
       [-0.0458467 , -0.10278892,  0.01064102, ...,  0.        ,
         0.        ,  0.        ],
       [ 0.14912559, -0.06840275,  0.00767626, ...,  0.        ,
         0.        ,  0.        ],
       [-0.04991312, -0.10697621,  0.00952425, ...,  0.        ,
         0.        ,  0.        ]])

.base_values =
array([0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332, 0.38372332, 0.38372332,
       0.38372332, 0.38372332, 0.38372332])

.data =
array([[ 3., 28.,  1., ...,  0.,  0.,  1.],
       [ 2., 31.,  0., ...,  0.,  0.,  1.],
       [ 3., 20.,  0., ...,  0.,  0.,  1.],
       ...,
       [ 3., 28.,  0., ...,  0.,  0.,  1.],
       [ 2., 24.,  0., ...,  0.,  0.,  1.],
       [ 3., 18.,  1., ...,  0.,  0.,  1.]])

18.1.1 Beeswarm Plot: Probability

shap.plots.beeswarm(shap_values_probability)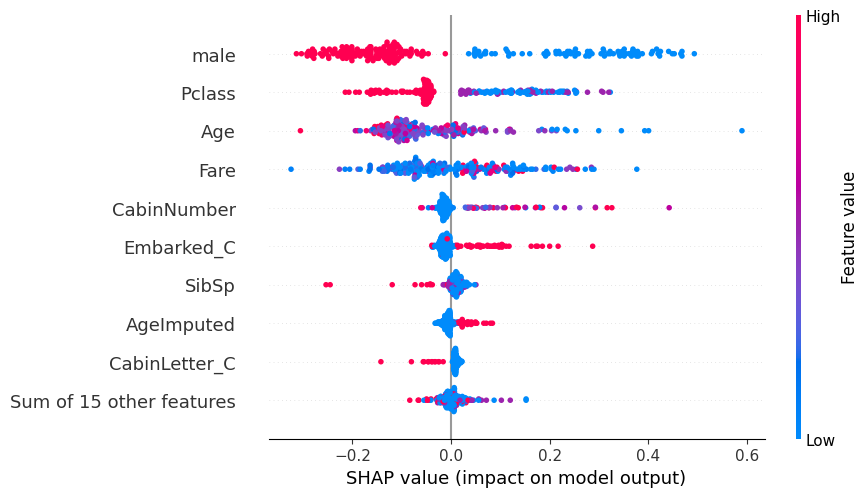

18.1.1.1 Comparison with log odds plot

fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1, figsize=(10,20))

plt.sca(ax1) ## NEW
shap.plots.beeswarm(shap_values, show=False)
plt.title("Log Odds")

# Change to the second axis
plt.sca(ax2) ## NEW
shap.plots.beeswarm(shap_values_probability, show=False)
plt.title("Probability")
plt.tight_layout()
plt.show()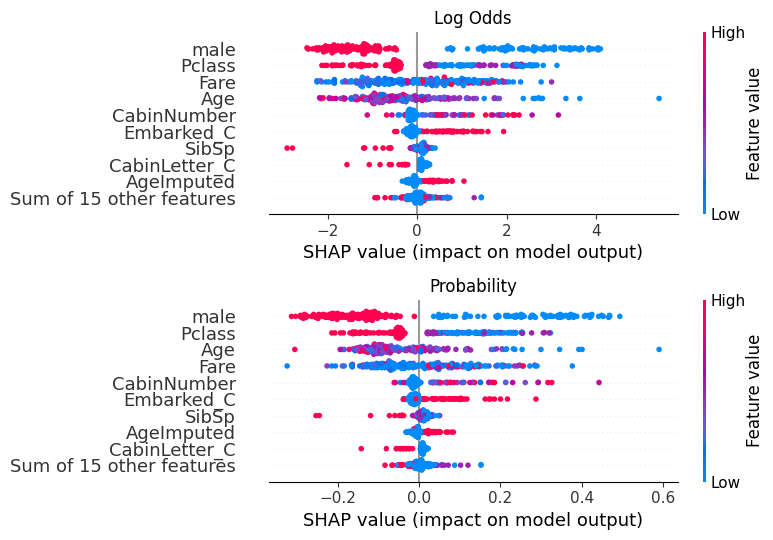

18.1.2 Waterfall Plot: Probability

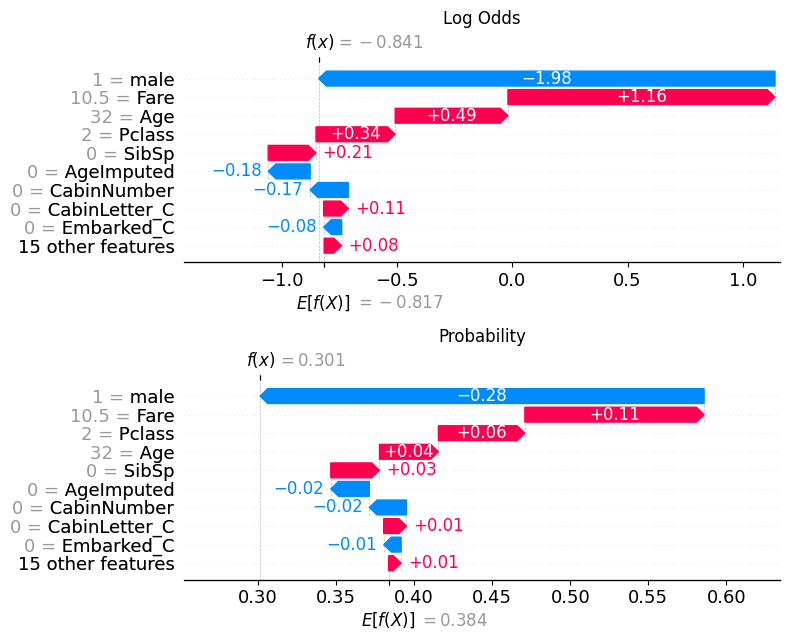
If we pull out the predicted probability for this passenger, we can see that the predicted probability of class 0 (died) is 0.69, while the predicted probability of survival (class 1) is 0.301.

pd.DataFrame(model.predict_proba(X_test)).reset_index(drop=True).iloc[56]
0    0.69867
1    0.30133
Name: 56, dtype: float32

This matches what is now shown in the waterfall plot.

shap.plots.waterfall(shap_values_probability[56])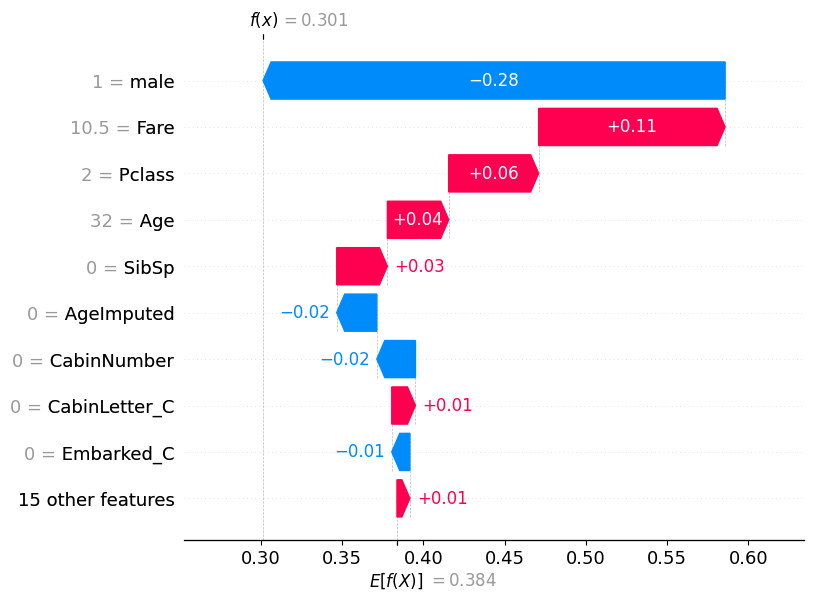

pd.DataFrame(model.predict_proba(X_test)).reset_index(drop=True).iloc[115]
0    0.97308
1    0.02692
Name: 115, dtype: float32
shap.plots.waterfall(shap_values_probability[115])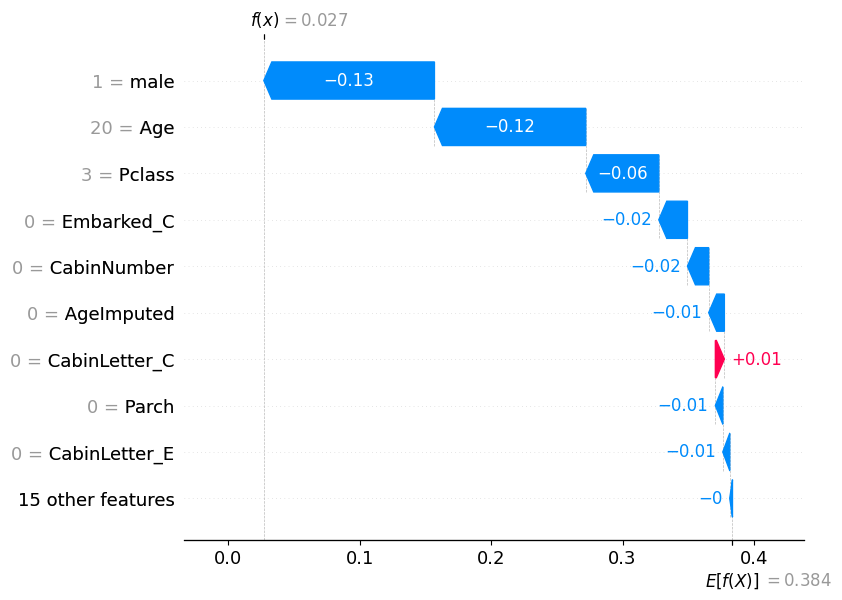

pd.DataFrame(model.predict_proba(X_test)).reset_index(drop=True).iloc[195]
0    0.000583
1    0.999417
Name: 195, dtype: float32
shap.plots.waterfall(shap_values_probability[195])

18.1.2.1 Comparison with log odds plot

fig, (ax1, ax2) = plt.subplots(nrows=2, ncols=1, figsize=(10,20))

plt.sca(ax1) ## NEW
shap.plots.waterfall(shap_values[56], show=False)
plt.title("Log Odds")
# Change to the second axis
plt.sca(ax2) ## NEW
shap.plots.waterfall(shap_values_probability[56], show=False)
plt.title("Probability")
plt.tight_layout()
plt.show()